什么是树

树是由n(n>=0)个结点组成的一个具有层次关系的有限集合。

如果n=0，它是一棵空树，这是树的特例；

如果n>0，它是一棵非空树。一棵非空树的示意图如图1所示。

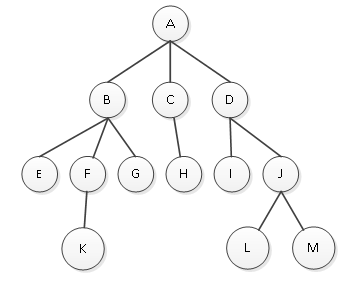
图1 树

图1就是一棵非空树，树中的每个元素称为结点。

在任意一棵非空树中，存在且仅存在一个根结点，简称根，根结点只有后继结点而没有前驱结点，图6-1中的A结点就是根结点；

其余结点可以分为多个互不相交的有限集，每一个有限集又是符合定义的树，称为根的子树。如以B结点为根，是一棵树；以J结点为根，是一棵树。因此树也可以说是由树根和若干棵子树构成。

树的定义具有递归性，因为在树的定义中又用到了树的定义，这是树的固有特性，即一棵树由若干棵互不相交的子树构成，而每一棵子树又是由更小的子树构成。

学习树，就必须要要学习树的一些基本术语，比如根、结点、叶子等，接下来我们就来学习树的一些相关术语。

在一棵树中，每个结点的直接后继结点称为该结点的孩子结点（子结点）。相应的，该结点称为孩子结点的双亲结点（父结点）。具有同一父结点的结点互为兄弟结点。进一步推广，隔了代的兄弟结点称为堂兄弟结点，而在垂直关系上，它们又称为子孙结点。以图6-1中的树为例：

①A是B、C、D的父结点；B、C、D是A结点的孩子结点；

②B、C、D是兄弟结点；E、F、G是兄弟结点；I、J是兄弟结点；

③E、H、I是堂兄弟结点；K、L是堂兄弟结点；

④以B、C、D为根结点的子树上的所有结点都是A结点的子孙结点；

⑤A、B、F都是K结点的祖先结点（具有垂直的直系关系）。

在树中，一个结点拥有的子树的数目称为结点的度，如图6-1中根结点A的度为3，因为它有B、C、D（以这三个结点为根结点的子树）三棵子树；D结点的度为2，因为它有I、J两棵子树；C结点的度为1，它只有以H为根结点的一棵子树。

树中各结点度的最大值称为树的度，通常将度为m的树称为m次树。如图6-1是一棵3次树，因为所有结点中度的最大值为3。

在一棵树中，度不为0的结点称为非终端结点或分支结点，度为0的结点称为终端结点或叶子结点，也就是没有后继结点的结点就是叶子结点。如图6-1中的树，B、C、D、F等都是分支结点，而E、H、K、L等都是叶子结点。对于分支结点，其分支数就是该结点的度。

树中的结点都处在某一个层次中，树的层次从根开始定义，根为第一层，根的孩子为第二层，以此类推，结点所在层次为其父结点层次加1。而树的最大层次为树的高度或深度。图1中的树有4层，树的高度为4，如图2所示。

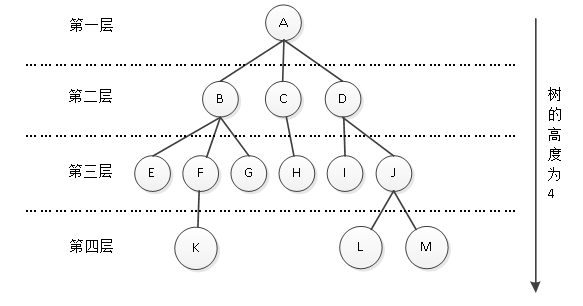
图2 树的层次与高度

若从树中的结点ki开始，沿着结点序列kikp…kj，可以找到结点kj，则称结点序列kikp…kj是从ki到kj的一条路径或道路，如图3所示。

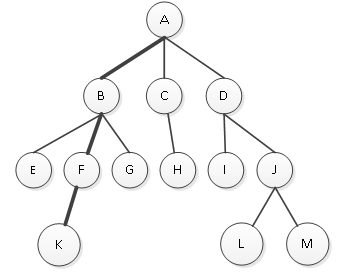
图3 结点A到K的路径

在图3中，描粗的部分就是结点A到结点K的路径，所谓路径其实就是从一个结点到达另一个结点的路线。路径的长度是路线上所经过的边（连接两个结点的线段）的数目，等于结点个数减1。

注意：若一个结点序列是路径，则在树的树形图表示中，该结点序列“自上而下”地通过路径上的每条边，从树的根结点到树中其余各结点均只有一条唯一路径。

多棵树可以组成一个森林，森林就是m(m>=0)棵互不相交的树的集合。对于树来说，其子树的集合就是森林，例如图2中的树，删除根结点A之后，其子树就组成了一片森林。

如果一棵树中的结点，从左至右是有序的，不能互换，则称这棵树为有序树。否则称为无序树。若无特别指明，一般讨论的都是有序树。在有序树中，最左边的子树称为根的第一个孩子，最右边的称为最后一个孩子。