平衡二叉树的概念

在学习二叉排序树的查找时，通过分析查找算法的效率可知，不同结构的二叉排序树查找效率有很大不同，单支树的查找效率相当于顺序查找，而越趋于平衡的二叉排序树查找效率越高。因此，在二叉排序树的基础上引入了平衡树二叉树（Balance Binary Tree）。

所谓平衡二叉树是指它除了具备二叉排序树的基本特征之外，还具有一个非常重要的特点：它的左子树与右子树的深度之差（平衡因子）的绝对值不超过1，且都是平衡二叉树。二叉树结点的左子树深度减去右子树深度的值称为平衡因子（Balance Factor）BF。那么平衡二叉树上的所有结点的平衡因子只可能是-1、0、1。只要二叉树上一个结点的平衡因子的绝对值大于1，那么该二叉树就不是平衡二叉树。

平衡二叉树是二叉排序树的一个进化体，也是第一个引入平衡概念的二叉树，它是由G.M. Adelson-Velsky 和 E.M. Landis提出的，所以它又被叫作AVL树。如图1所示。

图1 二叉排序树

在图1中有三棵二叉排序树，但只有树①是平衡二叉树，因为在树②中，根结点100的左子树高度为2，而右子树高度为0，其差值为2，因此不是平衡二叉树。在树③中，根结点100的右子树中有小于100的结点，它不是一棵二叉排序树，因此更不是平衡二叉树。

平衡二叉树也可以进行查找插入等操作，在进行查找操作时与二叉排序树相同且效率比二叉排序树高，如果平衡二叉树平衡度很高，则相当于是顺序表中的折半查找；

但在执行插入操作时要时时注意保持树的平衡性，在插入结点时，如果距离插入位置最近且平衡因子绝对值大于1的结点，以此为根结点的子树称为最小不平衡子树。例如有一棵平衡二叉树，如图2中①所示，现在往此树中插入一个新结点，如树②。

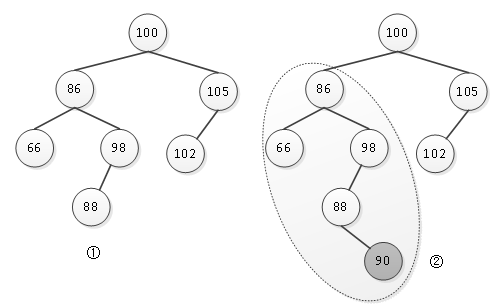
图2 最小平衡子树

树①是一棵平衡二叉树，向树中插入一个值为90的结点，这样就打破了树的平衡性，离插入位置最近且平衡因子绝对值大于1的结点是86，则以86为根结点的子树就是最小不平衡子树，如树②中虚线框内的子树，它就是此树中最小不平衡子树。