归并排序

归并排序(merging sort)，顾名思义，就是将两个序列合并在一起，并且使之有序。该算法是分治法的一个典型应用，其主要思想是将已有序的两个子序列合并，在过程中对其元素进行比较排序，从而得到一个完整有序的序列。也就是先保证小范围的数据有序，再使大范围的序列有序。

因此，若使用归并排序对一个序列进行排序，采用分治法思想，需要先将比较大的原始序列划分为较小的序列，使较小的序列有序。分出来的序列越小，对子序列的排序就越简单。比如对于每个序列只包含两个数据的序列，只要比较一次，就可以获得有序序列。

对于一个包含n个记录的序列，通常先将序列视为n个小序列，使相邻的两个小序列两两比较并归并，如此就有了 个次小的序列。每次排序归并都使子序列的数量减半，当子序列的数量为2时，再执行一次排序归并，就可以使原始序列成为一个有序序列。这样的方法称为2-路归并排序。如图1是对序列arr[]进行2-路归并排序的过程。

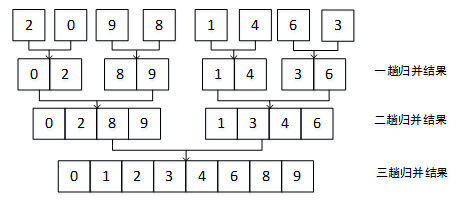
图1 2-路归并排序过程示例

图1中的原始序列为一个int型的数组arr[]，arr[8]= { 2, 0, 9, 8, 1, 4, 6, 3}。初始将数组arr[8]视为8个子序列，在第一趟归并中，将前后相邻的两个序列合并为一个有序序列，子序列的个数减少为4个；在第二趟归并中，执行同样的操作，子序列的个数减少为2个；在第三趟归并中，对上轮得到的两个子序列进行排序，序列的数量变为1个，该序列的归并排序过程结束，得到一个升序有序的序列。

归并排序需要一个原始序列大小的辅助空间，在排序归并的过程中，将本轮排序过程中的元素赋给中间变量，当排序结束之后，再从中间变量中取值赋给原始序列。若在排序的过程中，一个序列的数据已经排序完毕，另外一个序列还有数据剩余，此时可以终止比较，将序列中剩余数据逐个赋给中间变量。

假设需要归并的两个序列分别为sub1[]和sub2[]（这两个序列已各自有序），设其中元素的下标分别为i和j，元素个数分别为a和b；设置辅助空间变量tmp[]，其中元素对应下标为k。则归并步骤如下：

（1）初始时i=0，j=0，k=0。

（2）比较sub1[0]和sub2[0]：

a) 若sub1[0]>sub2[0]，使tmp[0]=sub2[0]，i=i+1，k=k+1；

b) 若sub1[0]<sub2[0]，使tmp[0]=sub1[0]，j=j+1，k=k+1；

（3）若i<a且j<b，则再次执行步骤(2)，否则比较结束。

（4）此时若其中一个序列的值全部赋值给中间数组，另一个序列中尚有元素未排序，将该序列中的值从arr[j]到arr[b-1]依次赋值给tmp数组中k以及之后的位置。

以序列sub1={0,2,6,7}和序列sub2={1,3,4,5,8,9}为例，演示上述归并过程。初始时创建辅助数组tmp，大小与原始序列大小相同。sub1[]、sub2[]和tmp[]的下标分别为i、j、k，初始值均为0，初始状态如图2所示：

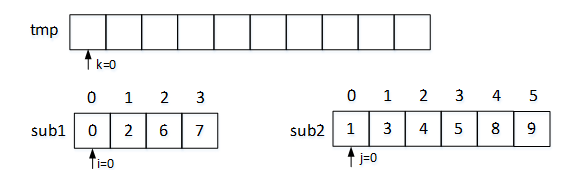
图2 初始状态

首先由sub1[0]和sub2[0]进行比较。因为sub1[0]<sub2[0]，所以将sub1[0]的数据赋给tmp[0]，使sub1[]的下标i+1，tmp[]的下标k+1。操作后的数组分别如下图3所示：

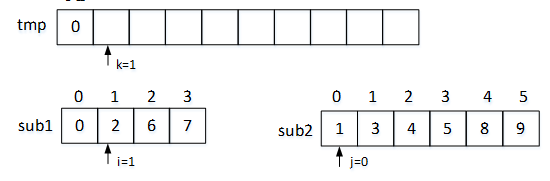
图3 第一次比较赋值结果

再次比较sub1[i]和sub2[j]，此时i=1，j=0，k=1。因为sub1[1]>sub2[0]，所以将sub2[0]赋给tmp[1]，使sub2[]的下标j+1，tmp[]的下标k+1。操作后的数组分别如下图4所示：

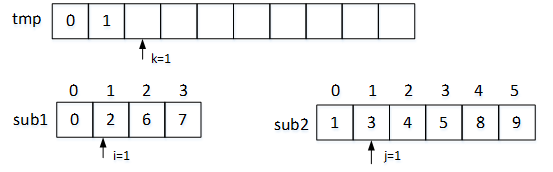
图4 第二次比较赋值结果

继续比较sub1[i]和sub2[j]，此时i=1，j=1，k=1。因为sub1[1]<sub2[1]，所以将sub1[1]赋给tmp[2]，使sub1[]的下标i+1，tmp[]的下标k+1。操作后的数组分别如下图5所示：

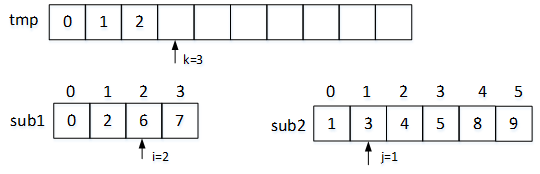
图5 第三次比较赋值结果

根据原则，第四次比较之后，sub2[1]被赋值给tmp[3]，j=j+1=2，k=k+1=4；第五次比较之后sub[2]被赋值给tmp[4]，j=j+1=3，k=k+1=5；第六次比较之后，sub[3]被赋值给tmp[5]，j=j+1=4，k=k+1=6；第七次和第八次比较，sub1[2]和sub1[3]分别被赋值给tmp[6]和tmp[7]，此时i=i+1=4，i已大于sub1[]的长度，所以sub1[]中的数据比较完毕；k=8，j=4，所以将sub2[]中从sub2[4]开始到末尾的数据依次赋给tmp，即使tmp[8]=sub2[4]，tmp[9]=sub2[5]。至此tmp[10]={0,1,2,3,4,5,6,7,8,9}，对于两个序列的归并与排序结束。

在平时使用归并算法时，往往是对一个原始序列的拆分与归并，拆分出的序列对应原序列中的下标，可能不为0，所以要根据实际情况赋值，其它规律都与以上过程相同。

结合上述分析，给出归并两个序列的算法实现。

//归并两个序列的算法
void Merge(int arr[], int tmp[], int start, int mid, int end)
{
    int i = start, j = mid + 1, k = start;
    //比较排序并将值赋给中间变量tmp
    while (i != mid + 1 && j != end + 1)
    {
        if (arr[i] >= arr[j])
            tmp[k++] = arr[j++];
        else
            tmp[k++] = arr[i++];
    }
    //若一个序列指针走到最后，另一个指针为走到最后，直接复制
    while (i != mid + 1)
        tmp[k++] = arr[i++];
    while (j != end + 1)
        tmp[k++] = arr[j++];
     //将中间变量数组中存储的值赋给原始数组
    for (i = start; i <= end; i++)
        arr[i] = tmp[i];
}

2-路归并排序算法在每一趟归并中调用上面的归并函数，其算法是一个递归算法。下面给出2-路归并排序算法的实现。

//递归调用归并算法
void MergeSort(int arr[], int tmp[], int start, int end)
{
    int mid;
    if (start < end)
    {
        //取中间值将原序列分为两组
        mid = (start + end) / 2;    
        MergeSort(arr, tmp, start, mid);
        MergeSort(arr, tmp, mid + 1, end);
        Merge(arr, tmp, start, mid, end);
    }
}

在2-路归并排序算法中，由于需要进行递归调用，为了保证递归的顺利执行，按照一定的方法划分序列，直到子序列成为单个的元素，才开始对相邻的序列进行排序与归并。

通常根据二分思想将序列划分为两个长度基本相同的序列：设序列的最低位为start，最高位为end，设置一个辅助变量mid，用来保存分组信息，通常使mid=(start+end)/2，如此序列[start，end]被划分为子序列[start,mid]和[mid+1,end]。若子序列中的元素不唯一，则继续使用此方法对每个子序列进行划分。

以序列arr[8]= { 2, 0, 9, 8, 1, 4, 6, 3}为例，划分序列的过程如图6所示。

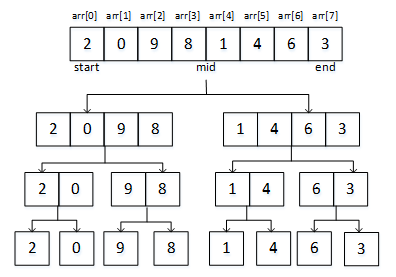
图6 序列分组过程图

使用归并排序算法时，一趟归并需要将序列中的n个有序小序列进行两两归并，并且将结果存放到中间数组tmp[]中，这个操作需要扫描序列中的所有记录，因此耗费的时间为O(n)。由图9-39可以看出，归并排序过程中的序列分组类似于一棵树，所以归并排序需要进行log2n次。因为这两种操作是嵌套关系，所以归并排序算法的时间复杂度为O(nlog2n)。

另外归并排序需要与原始序列同样数量的存储空间，所以其空间复杂度为O(n)；Merge函数中的if语句表明序列中的数据需要两两比较，不存在跳跃交换，因此该算法是一个稳定的算法。

归并排序的递归求解代码结构清晰，易于理解，但是造成了空间和时间上的浪费，其性能有一定损耗，所以在平常的求解中，通常不使用递归的归并排序算法。