链式基数排序

基数排序借助多关键字排序和分配式排序的思想，对单关键字的序列进行排序。

所谓借助多关键字排序思想，是将一个单关键字，视为多个关键字。例如对于数字0~999，可以把每一位上的十进制数字都视为一个关键字，不足三位的两位数和一位数，在它们的高位补零，使其成为三位数，这样原本关键字为一千以内数字的序列，就可以视为有三个10以内数字关键字的序列；对于由多个大写字母组成的字符串，可以将每一个字母视为一个关键字，这样每一条记录都可以视为有多个关键字的序列。

若由一个多位关键字分出的多个单位关键字，每一个关键字的范围都在[0,r]之间，那么r称为基数。排序的轮数由所有序列中关键字位数最多的关键字决定，这个关键字的位数就是排序需要进行的轮数。

此时使用LSD进行排序，只要从最低位关键字开始，按照关键字的值将原始序列中的记录分配到多个“桶”中（这个“桶”由关键字范围确定）再依次收集，组成新的序列，然后按照次低位的关键字重新将记录分配并收集，如此重复操作，直到按照最高位关键字对序列分配收集完毕，方可获得一个按关键字有序的序列。

这种方法结合了多关键字排序和桶排序，在使用多关键字排序思想的基础上解决了桶排序中时间效益与空间效益不可兼得的矛盾。对10个一千以内的整数，使用桶排序时，若每个桶中存储的键值依次加1，那么这10个数据会被分配到这1000个桶中，显然很多桶都为空；使用基数排序时，一千以内的整数被视为由三个0~9之间的数字组成的数据，关键字的范围从原来的0~999缩小到了0~9，只需要根据每一位的数字，对这10个一千以内的数进行三次分配与收集，就能得到我们需要的序列。

下面以字符数组arr[10]={“012”, “398”, “045”, “571”, “036”, “002”, “653”, “859”, “092”, “126”}为例，通过图示来演示使用链式存储来进行基数排序的过程。通过上一小节桶排序的学习可以了解到，桶排序中每个桶将会存储的数据量不定，所以在这里，使用链表的方式来表示每个桶中的数据。

首先给出链表结点的结构定义，由以上分析可知，结点中需要存放结点数据，和指向下一个结点的指针，结点的关键字包含在结点数据中。为了简化学习，使结点中的关键字同时代表结点数据。因为需要对关键字的每一位进行一次排序操作，所以使用一个数组来存储关键字，记为keys[]，结点中的数据从高位到低位依次存放在数组key[]中。

结点的结构定义如下，其中MAXD定义了关键字的最大位数。

#define MAXD 8            //关键字的最大位数
typedef struct node
{
    char keys[MAXD];    //关键字字符串
    struct node *next;
} RecType;

首先使用单链表存储数据，则数组arr[]的存储结构如图1所示。

图9-1 数组arr[]的链式存储

因为关键字的范围为0~9，所以创建10个“桶”，每个桶是一个链表，分别存储分组时关键字相同的记录。为了保证排序的稳定性，在分配数据时，应将后入的数据放在桶中已有数据之后，所以在这里使用尾插法将数据添加到桶中。这要求每个桶链表既有表头指针，也有表尾指针。

下面进行第一轮排序。在第一轮排序中，首先根据关键字的个位数，也就是key[2]，对数据进行分配。一轮分配过后，每个桶链表中存储的数据如图2所示。

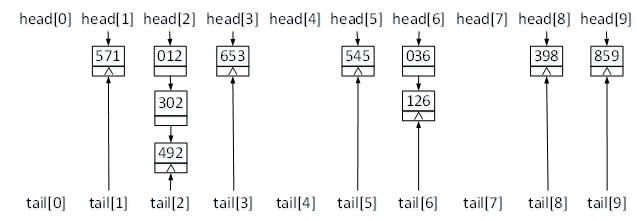
图2 一轮排序分配结果

其次对一轮分配结果进行收集，使不为空的桶链表数据依次链接，即使当前桶链表中最后一个数据的指针指向下一个不为空的桶链表的第一个数据，如此便可得到一轮排序的最终结果。一轮排序结果如图3所示。

图3 一轮排序结果

然后进行第二轮排序。在第二轮排序中，首先对一轮排序结果按照其十位上的数据，也就是key[1]，进行分配，每个桶中存储的数据如图4所示。

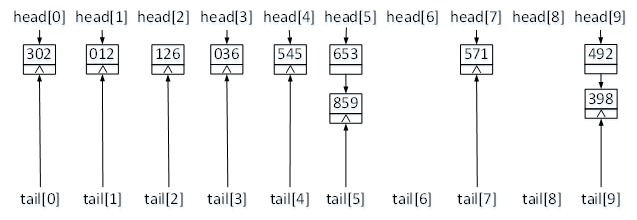
图4 二轮排序分配结果

其次对图4中二轮排序的分配结果进行收集，产生的链表如图5所示。

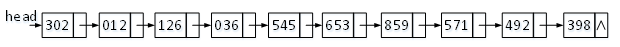
图5 二轮排序结果

最后进行第三轮排序，因为数据中位数最多为3位，所以排序只需要进行三轮。在第三轮排序中，首先对二轮排序结果按照其百位上的数据，也就是key[0]，进行分配，每个桶中存储的数据如图6所示。

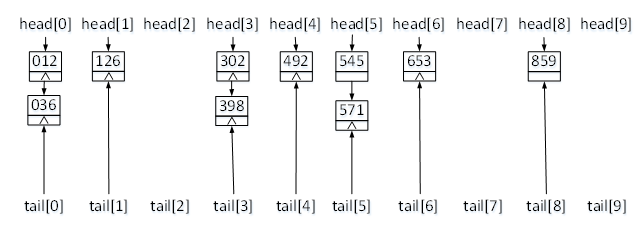
图6 三轮排序分配结果

其次对分配结果进行收集，产生的链表如图7所示，此次收集完成之后，得到一个升序有序的链表。

图6 排序结果

至此，对数组arr[]进行的基数排序操作已全部完成。下面给出链式基数排序算法的代码实现。

//基数排序
//p为待排序序列链表的指针,r为基数，d为最大关键字的位数
void RadixSort(RecType *&p, int r, int d)
{
    RecType *head[MAXR], *tail[MAXR], *t;    //定义各桶链的首尾指针
    int i, j, k;
    for (i = d - 1; i >= 0; i--)               //从低位到高位依次排序
    {
        for (j = 0; j<r; j++)                 //初始化桶链表的首尾指针
            head[j] = tail[j] = NULL;
        //数据分配
        while (p != NULL)                      //对链表中的每个结点循环判断
        {
            k = p->keys[i] - '0';           //找到关键字对应的桶链表
            if (head[k] == NULL)               //采用尾插法进行分配，将结点加入桶链
            {
                head[k] = p;
                tail[k] = p;
            }
            else
            {
                tail[k]->next = p;
                tail[k] = p;
            }
            p = p->next;                     //继续取值
        }
        p = NULL;
        //数据收集
        for (j = 0; j<r; j++)                
        if (head[j] != NULL)             
        {
            if (p == NULL)
            {
                p = head[j];
                t = tail[j];
            }
            else
            {
                t->next = head[j];
                t = tail[j];
            }
        }
        t->next = NULL;                        //最后一个结点的指针域置空
    }
}

对基数排序算法进行分析：在基数排序的过程中，共进行d趟分配和收集，每一趟分配和收集的时间复杂度为O(n+r)，所以基数排序的总时间复杂度为O(d(n+r))。

基数排序算法借助的辅助空间由桶的个数决定，每一趟排序中使用r个辅助空间。又因为每一趟排序的关键字相同，所以这些辅助空间可以重复使用，也就是说，基数排序算法的空间复杂度为O(r)。