广度优先遍历
广度优先遍历(Breadth First Search)类似于树的按层遍历。它的基本思想是:任意选定一个顶点v开始本次访问,在访问过v之后依次访问v的待访问(尚未被访问)邻接点,并将已访问的顶点放入队列Q。按照Q中顶点的次序,依次访问这些已被访问过的顶点的邻接点。如果队头的顶点不存在待访问邻接点,让队头顶点出队,访问新队头的待访问邻接点,如此直到队列为空。
广度优先遍历同样需要一个状态数组visited[]。执行到此处,如果图是连通图,那么图中所有的顶点此时应均已被访问;如果图非连通图,此时队列Q为空,但visited[]数组中应有顶点为未被访问状态,需另选一个未被访问的顶点,对其再次执行广度优先遍历过程。
广度优先遍历算法不是一个递归的过程。当然它可以写成递归,但是没有这个必要。因为递归的过程中系统开辟栈空间作为临时变量的存储空间,但是广度优先遍历需要的是一个队列,所以这个算法不追求递归。
以图1中的无向图G为例。为了简化要学习的内容,对图G做出调整,使它看起来层次分明,更接近一棵树,当然图G的逻辑结构并未有任何改变。以顶点A作为起始点,调整后的图G如图1所示。
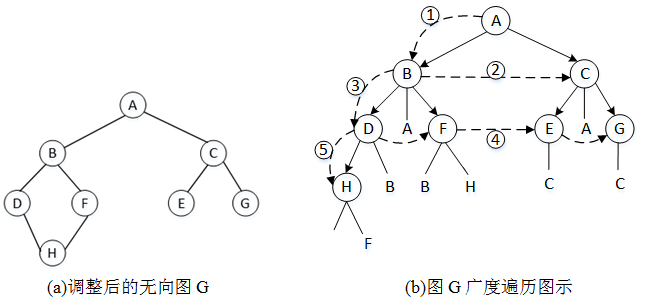
图1 广度优先遍历示例
参照图7-17(b)理解广度遍历的基本思想:首先访问顶点A,将顶点A的状态修改为已访问,并让顶点A进入队列。然后按照从左往右的顺序依次访问A的邻接点(这个顺序是任意的,只是为了便于讲解才做出的规定,读者应明白图中的顶点没有层级与先后之分),也就是B、C。在访问的过程中需要修改状态数组visited[]中与顶点对应的状态信息,并将已访问的顶点放入队列Q。
此时队列中元素从头到尾依次为:A、B、C,队头元素A的邻接点也已全部访问完毕。让队头A出队,之后去访问新队头B的待访问邻接点。B的邻接点分别为D和F,访问完毕之后,队列中的数据为:B、C、D、F。
此时队头B的邻接点访问完毕,按照上一步中的规则与队列中数据的顺序,继续执行“出队——访问队头邻接点”这一操作,直到队列为空,与A连通的所有顶点访问完毕。
因为图G是一个连通图,所以此时图G的所有顶点均已被访问,得到的顶点访问序列为:A->B->C->D->F->E ->G->H。若G是非连通图,此时G中不包含顶点A的其它连通分量尚未被访问,此时选取待访问顶点中的任意一个作为端点,再次执行广度优先遍历过程即可。
下面用C语言代码来实现广度优先遍历的算法。代码中涉及到了队列的知识,这些知识在第三章有详细的讲述,因此这里用到的接口函数就不再重新定义。
//①基于邻接矩阵的广度优先遍历
void BFS(Graph G)
{
int i, j;
SeqQueue Q = Create(); //创建存储顶点的队列并初始化
for (i = 0; i < G.n; i++) //初始化状态数组
visited[i] = 0;
for (i = 0; i < G.n; i++)
{
if (visited[i] == 0) //若是未访问的顶点
{
visited[i] = 1;
printf("%d ", G.vexs[i]);
Insert(&Q, i); //入队
while (!isEmpty(Q)) //若当前队列不为空
{
Del(Q); //出队
for (j = 0; j < G.n; j++)
{
//访问当前顶点的待访问邻接点
if (G.edges[i][j] == 1 && visited[j] == 0)
{
visited[j] = 1; //修改访问状态
printf("%d ", G.vexs[j]);
Insert(&Q, j); //入列
}
}
}
}
}
}
---------------------------------------------------------------------
//②基于邻接表的广度优先遍历
void BFS(GraphAdjList GL)
{
int i;
EdgeNode *p;
SeqQueue Q = Create(); //创建一个存放顶点的队列
for (i = 0; i < GL.n; i++)
visited[i] = 0; //初始化访问状态
for (i = 0; i < GL.n; i++)
{
if (!visited[i])
{
visited[i] = 1;
printf("%d ", GL.adjList[i].data);
Insert(&Q, i); //入队
while (!isEmpty(Q))
{
Del(Q); //出队
//找到当前顶点边表链表头指针
p = GL.adjList[i].firstedge;
while (p)
{
if (visited[p->adjvex] == 0) //若此顶点未被访问
{
visited[p->adjvex] = 1;
printf("%d ", GL.adjList[p->adjvex].data);
Insert(&Q, p->adjvex); //入队
}
p = p->next;
}
}
}
}
}针对广度优先遍历的两种算法之间的差异也是由于图的基础存储结构不同。它们和对应结构深度优先遍历算法的时间复杂度相同:邻接矩阵存储时时间复杂度仍为O(n2),邻接表存储时时间复杂度仍为O(n+e)。所以这两种遍历方式并无优劣之分,只是重点不同。深度优先算法倾向于查找具体而明确的目标,而广度优先算法倾向于在扩大范围的同时寻找相对最优解。
