树的表示法

通常树有三种表示方法：图形表示法，广义表表示法和左孩子右兄弟表示法。接下来分别讲解如何用这三种方法来表示一棵树。

1、图形表示法

图形表示法是树结构最常用的表示方法，在树形图表示中，结点用圆圈表示，元素名称写在圆圈中，各结点之间的关系用连接线来表示。图1、图2都是用图形来表示一棵树，这种表示方法直观、清晰、易于理解，最为常用，这里不再过多讲解。

2、广义表表示法

我们知道广义表是多层次的线性结构，用它也可以来表示出树形结构。用广义表来表示树形结构时，根结点写在最外层，即表的最左边，第一层是其直接孩子结点，第二层是其孙子结点，这样逐层深入。假如有一棵表示中国省市关系的树，如图1所示。

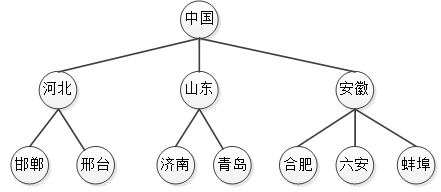
图1 省市关系图

用广义表来表示这棵树，则这棵树表示为：（中国（河北（邯郸，邢台），山东（济南，青岛），安徽（合肥，六安，蚌埠）））。广义表的最外层是根结点“中国”，第二层里是根结点的孩子“河北”、“山东”、“安徽”，再往里一层则是第二层中结点的孩子。

同样，如果用广义表来表示图6-1中的树，第一步先写出根结点A与其孩子结点，如下所示：

(A(B,C,D))

然后再写出B，C，D结点的孩子结点，如下所示：

(A(B(E,F,G),C(H),D(I,J)))

最后再写出第三层结点的孩子结点，如下所示：

(A(B(E,F(K),G),C(H),D(I,J(L,M))))

这就是树的广义表表示法，其实也比较简单，它一般较多的应用是给出广义表，让画出其对应的树形结构图，如例1所示。

例1

有一棵广义表表达的树：(12(32(5,65(31,0))，100,54(85,664)))，请根据此表画出相应的树形结构。

推导过程如下：

（1）表第一层只有12，可知12为此树的根结点；

（2）表的第二层有32、100、54三个结点，这三个结点就是根结点的孩子结点；其结构如图2所示。

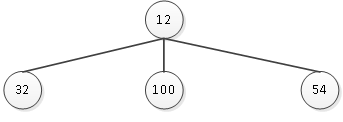
图2 第一层与第二层结点

（3）表的第三层中，结点32有5和65两个孩子结点；结点100无孩子结点；结点54有85和664两个孩子结点；其结构如图3所示。

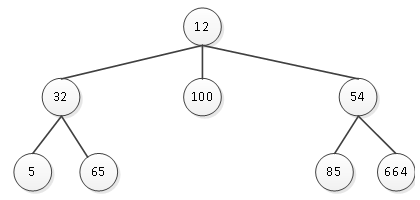
图3 第一、二、三层结点

（4）表的第四层，结点65有31和0两个孩子结点，其他结点无孩子；则其结构如图4所示。

图4 完整的树

再往更深层次看，各结点都再无孩子结点，则图4就是此表对应的完整的树。

3、左孩子右兄弟表示法

树的左孩子右兄弟表示法，类似于中国的长兄如父的思想，它指的是由左边的孩子结点来接管右边的孩子结点，类似于年长的孩子照管年幼的孩子。以图6-1中的树为例演示左孩子右兄弟表示法。

（1）根结点A有三个孩子，则将右边的孩子结点托管给左边的孩子结点，如图5所示 。

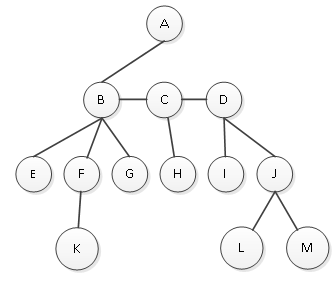
图5 将结点A的孩子托管

（2）继续调整。结点B有三个孩子E、F和G；结点C有一个孩子H；结点D有两个孩子I和J，则分别将右边的孩子托管给左边的孩子，如图6所示。

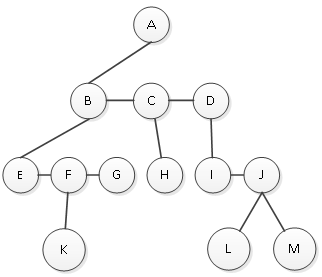
图6 左孩子右兄弟表示法

（3）调整更深层次，结点G有一个孩子K；结点J有两个孩子L和M，将M托管给L，如图7所示。

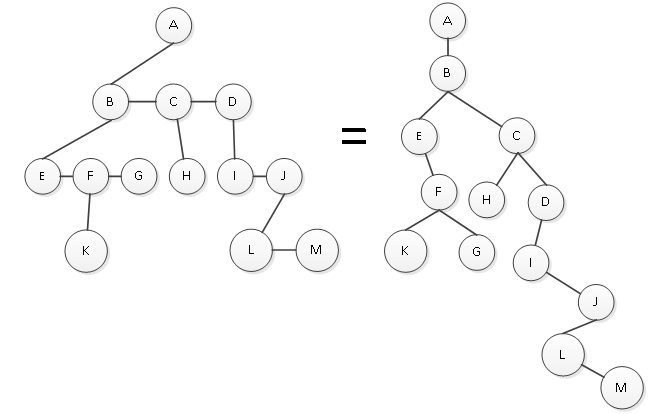
图7 左孩子右兄弟表示法

最终转换之后的结果就是图7所示的树，由此可见，左孩子右兄弟表示法可以将一棵多叉树转化为一棵二叉树。关于二叉树的概念，在下一节中会详细讲解，在这里读者只要知道二叉树在进行运算时比多叉树效率要高得多，将多叉树转换成二叉树更有利于树的各种运算即可。