B树的删除

在删除元素时同样需要先查找树中是否有此元素，如有则可以删除。在删除时要考虑待删除元素的结点是否是叶子结点，删除之后结点中的关键字的个数是否满足要求，如果不满足要求要作何处理，接下来举例展示如何删除一棵B树中的元素。现有一棵5阶B树，如图1所示。

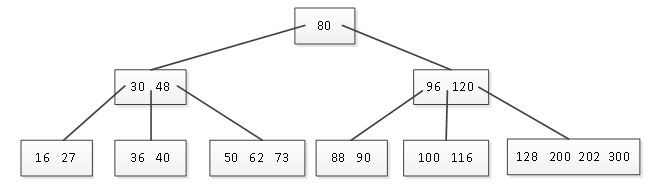
图1 5阶B树

这是一棵5阶B树，每个结点中关键字的个数要求是2-4个，在删除时要保证结点中的关键字

个数不能少于2。接下来以依次删除这棵B树中的50、120、100、36。

​ （1）删除50。经过查找得知50在一个叶子结点中，而且该结点中关键字个数为3，当删除50后，结点中关键字个数还满足要求，那么此时操作很简单，直接删除50即可，删除后的B树如图2所示。

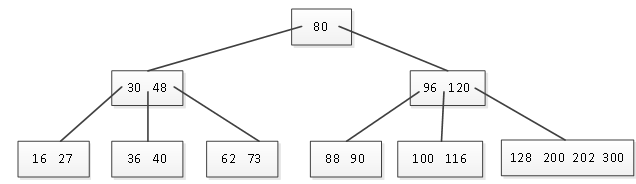
图2 删除50后的B树

（2）删除120。120所在的结点非叶子结点，它有左右孩子，而且删除120之后，结点中只剩

下96一个关键字，陷入了“贫困”（5阶B树要求除了根结点外，每个结点中至少要有2个关键字）。此时的解决办法是借用孩子结点中的关键字，可以将左孩子中最右边的关键字（116）上移到120的位置，补上120的空缺；或者是将右孩子中最左边的关键字（128）上移到120的位置补上空缺。

​ 若用116来补120的空缺，那么116原来所在结点只剩下一个关键字，又陷入“贫困”，而用128上移来补120的空缺，原来的结点中还有3个关键字，符合要求，因此可以用128来替补120，删除后的B树如图3所示。

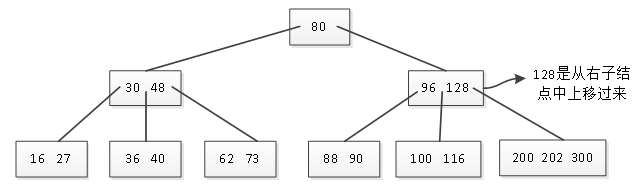
图3 删除120后的B树

（3）删除100。100所在结点为叶子结点，且结点中关键字个数为2，删除后只剩一个关键字，

已经小于所要求的最小数目。对于这种情况，如果其相邻兄弟（注意是相邻，隔结点的不算）结点中有比较“富裕”的，则可以向父结点借用一个关键字，然后将“富裕”兄弟结点中的一个关键字上移到父结点中。

​ 因为在删除100时，其右边相邻的兄弟结点比较“富裕”，所以可以向父结点借用128，然后将右边结点中的200上移到父结点中，删除100后的B树如图4所示。

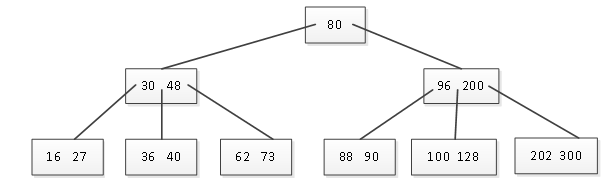
图4 删除100后的B树

（4）删除36。删除36会导致很多问题，因为36所在结点只有两个关键字，其父结点及相邻

兄弟结点也都是刚刚“脱贫”，并不“富裕”，无法借用。这种情况下就需要将结点与相邻的兄弟结点进行合并，首先将父结点中的关键字（此关键字是需要合并的两个结点的分界）下移到被删除的结点中，然后将两个结点进行合并。

​ 综上，在删除36时，考虑将它与左边的兄弟结点合并，则将父结点中的30下移到36的位置，然后将两个结点合并，如图5所示。

图5 相邻结点合并

但此时删除操作并没有完成，因为父结点中只剩下一个关键字，不符合标准。而此时父结点的兄弟结点也不“富裕”，无法借元素给它。这种情况下只能继续与兄弟结点合并。将更上一层的父结点中的关键字（80）下移到48所在的结点，然后与兄弟结点合并，如图6所示。

图6 删除36之后的B树

此时才算完成36的删除操作，持续的合并结点需要不断向父结点借用关键字，最终树的高度减

少一层。

至此，B树的删除操作也已经讲解完毕，总的来说，删除的操作要领是：如果“富裕”就直接删除，不“富裕”就先父子之间转借，如果还不够再兄弟之间转借合并。