希尔排序

希尔排序(shell sort)也是插入排序算法的一种，是直接插入排序更加高效的改进版本。该算法由DL·Shell于1959年提出。

无论是直接插入排序还是折半插入排序，都是将待排序序列视为一个分组。而希尔排序将原始序列，按照下标的一定增量分为多个序列，在每个序列中执行直接插入排序。随着增量的减小，每组包含的数据越来越多，当增量减至1时，所有的分组重新整合为一个序列，此时排序结束。

折半插入排序减少了数据的比较次数，但是没有提高数据移动的效率，对于几乎已经排好序的、需要少量移动的序列，直接插入排序效率较高，但是总体来说，这两种插入排序效率还是比较低的，因为插入排序在需要移动时，每次只能移动一位。希尔排序既解决了比较次数的问题，又解决了移动位数的问题。

希尔排序的基本思想是：先取定一个小于n的整数d1作为第一个增量，把序列的全部元素分成d1个组，所有相互之间距离为d1整数倍的元素放在同一个组中，在各组内进行直接插入排序；然后，取第二个增量d2（d2<d1)，重复上述的分组和排序过程，直至所取的增量dt=1(dt<dt-1<…<d2<d1），即所有元素放在同一组中进行直接插入排序。

下面以数组int arr[10]={ 2, 0, 9, 8, 1, 4, 6, 3, 7, 5 }为例，详细展示希尔排序过程中数据的分组情况和各组数据的排序过程。

在开始分组之前，首先需要确定一个增量d，这个增量决定了划分的组数，和初始时每组中元素下标相隔的距离。假设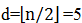，增量d的涵义为：数组arr[]将被分为5组，所有相互之间距离为5的倍数的元素放在同一组中。

例如设下标为idx，对于数组元素arr[0]，与它同组的元素其下标满足idx=0+5a(a=1,2,…)，因为idx的取值范围为[0,9]，所以与arr[0]同组的元素只有arr[6]。按照这样的规律，arr[]被分为{arr[0],arr[5]}，{arr[1],arr[6]}，{arr[2],arr[7]}，{arr[3],arr[8]}，{arr[4],arr[9]}这5个子序列。如图1所示。

图1 数组arr[]分组示意

对初始序列中的每个分组执行一次直接插入排序。

第一轮排序中：

（1）首先对第一个子序列{arr[0],arr[5]}进行直接插入排序，排序之后的子序列为{4,…,2,…}，数组arr[]的结果为{4, 0, 9, 8, 1, 2, 6, 3, 7, 5 }；

（2）其次对第二个子序列{arr[1],arr[6]}进行直接插入排序，排序之后的子序列为{…,6,…,0,…}，数组arr[]的结果为{4, 6, 9, 8, 1, 2, 0, 3, 7, 5}；

（3）然后对第三个子序列{arr[2],arr[7]}进行直接插入排序，由于子序列中的数据arr[2]=9，arr[7]=3，arr[2]>arr[7]，已经符合降序排列，所以子序列中的数据顺序不发生变化，本轮排序数组arr[]中的数据顺序也不发生改变。

（4）之后对第四个子序列{arr[3],arr[8]}进行直接插入排序，子序列{…,8,…,7,…}也已符合降序排列，子序列顺序和数组中数据顺序均不发生改变。

（5）最后对第五个子序列{arr[4],arr[9]}进行直接插入排序，排序之后的子序列为{…,5,…,1,…}，数组arr[]的结果为{4, 6, 9, 8,5, 2, 0, 3, 7, 1}。

一轮排序结果为：arr[10]={4, 6, 9, 8,5, 2, 0, 3, 7, 1}。

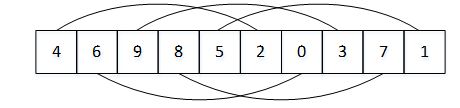
图2 一轮排序结果

随后进行第二轮排序：使增量，则d=2。对一轮排序结果进行分组，其结果被分为两组，分组情况如图3所示。

图3 二轮排序分组情况

在二轮排序中，分别对每组数据进行直接插入排序，排序后的数组为arr[10]={9,8,7,6,5,3,4,2,0,1}。

图4 二轮排序结果

此时数组中的arr[0]~arr[4]已经为降序排列，其余的数据也基本有序（在以降序序列为目标的排序中，基本有序指较大的数据基本处于序列前半段，较小的数据基本处于序列后半段，允许小范围内位置浮动。例如在图9-18的结果中，较小的arr[5]排在较大的arr[6]之前，较小的arr[8]排在较大的arr[9]之前。但不会出现本应该放在arr[0]的数据9，处于arr[9]的位置的情况）。最后进行第三轮排序：使增量，d=1，数据划分为1组，所以当前数组即为分好组后的数组，对整个数组进行一次直接插入排序，经过小幅度的位置变换，得到了一个按降序有序的数组，arr[10]={9,8,7,6,5,4,3,2,1,0}。

图5 三轮排序结果

在第三轮排序中，只有arr[5]和arr[8]分别移动了一次。至此使用希尔排序对数组arr[]排序已经结束了，也已得到了一个降序有序的序列。

下面给出希尔排序的算法实现。

//希尔排序
void ShellSort(int arr[], int n)
{
    int i, j, d;
    int tmp;
    d = n / 2;        //设置增量初值
    while (d > 0)
    {
        for (i = d; i < n; i++)    //对所有相隔d的元素组进行直接插入排序
        {
            tmp = arr[i];
            j = i - d;
            while (j >= 0 && tmp > arr[j])//对每组中的数据进行排序
            { 
                arr[j + d] = arr[j];
                j = j - d;
            }
            arr[j + d] = tmp;
        }
        d = d / 2;
    }
}

希尔排序的核心算法仍然为直接插入排序，但是希尔排序比直接插入排序多设置了一个步长增量，从而有效地减少了每轮排序比较的次数和比较的轮数，明显降低了时间消耗。

希尔排序的性能分析比较复杂，它的时间复杂度与设置的增量有关，然而如何取其增量尚无定论。但是无论如何选择，最后一个增量必须为1。按照上文中取增量的方法：d1= ，di=⌊di-1/2⌋（i>=1），即后一个增量为前一个增量的1/2，经过t=log2(n-1)次后，dt=1。希尔排序的时间复杂度难以估算，通常认为是O(n1. 3)。与前面介绍的插入排序算法相比，其时间性能的提升是可观的， 希尔排序是真正在时间复杂度上有数量级缩减的算法。

另外，希尔排序是个不稳定的算法。下面来举例说明。

以图6中的序列为例，其中有两个8，根据脚标区分。

图6 稳定性分析参考图示

假设初始增量d=3，第一组数据为{9,81,…}，第二组数据为{1,82,…}，显然在排序过程中第一组的8相对于9不会移动，而第二组的8会被插入到当前1所在位置，也就是第二个8将会被排在第一个8之前。结果如图7所示。

图7 一次交换结果

所以，希尔排序是不稳定的。