二叉树的分类

根据二叉树中子结点的排布，可将二叉树分为非完全二叉树、完全二叉树和满二叉树。

非完全二叉树是普通的二叉树，如上一节中的图1就是一棵非完全二叉树。

完全二叉树：除最后一层外，每一层上的结点数均达到最大值；在最后一层上只缺少右边的若干结点。如图1所示。

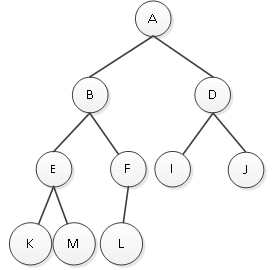
图1 完全二叉树

图1中是一棵完全二叉树，最后一层的结点都优先填在左边。若结点L在结点F的右侧，则该树不是完全二叉树。

对于完全二叉树来说，它有以下特点：

● 叶子结点只能出现在最下两层；

● 最下层的叶子结点一定集中在左边连续位置；

● 如果结点的度为1，那么该结点只有左孩子，不存在只有右孩子的情况；

● 同样结点数的二叉树，完全二叉树的深度最小。

满二叉树：除叶子结点外，树中的每个结点都有两个孩子结点，每一层的结点数都达到最大。如图2即为一棵满二叉树。

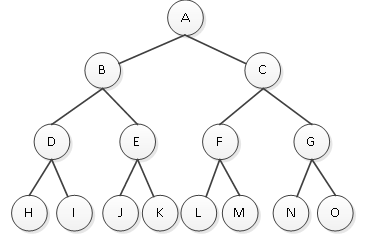
图2 满二叉树

图2中的二叉树，每一层结点数都达到最大，没有出现“缺胳膊少腿”的现象，在同样深度的二叉树中，满二叉树的结点最多。如果一棵深度为k的二叉树有2k-1个结点，那么这就是一棵满二叉树。

满二叉树是完全二叉树的特殊情况，可以说满二叉树也是一棵完全二叉树，但不能说完全二叉树是满二叉树。

斜树：一棵只有左孩子或者只有右孩子的树叫作斜树。只有左孩子的二叉树称作左斜树，只有右孩子的二叉树叫作右斜树。如图3所示。

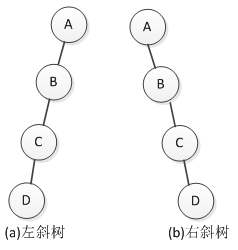
图3 斜树

斜树的每一层都只有一个结点，结点的个数与二叉树的深度相同。仔细观察发现，斜树与线性表结构是相同的，其实线性表可以看成是树的一种特殊形式。