图的定义与基本术语

1、图的定义

图（Graph）是一种数据结构，将其简化为顶点（Vertrx）和边（Edge）的组合，采用形式化的定义，定义一个图：

Graph=(V,E)

其中V为顶点的有限集合，V={x|x∈dataobject}，记为V(Graph)；E是边的有限集合，表示两个顶点之间的关系，E={<x,y>|x,y∈V}，记为E(Graph)。

2、图的基本术语

（1）顶点、邻接点、有向图、无向图

若有P<x,y>∈V表示在顶点x与顶点y之间的一条连线，则称x、y为该边的两个顶点，同时称x与y互为邻接点，即顶点x是顶点y的邻接点，顶点y也是顶点x的邻接点。称边P<x,y>依附于顶点x和顶点y，或者说边P<x,y>与顶点x、顶点y相关联。

若这条线从x指向y，则称x为起始点（弧头），称y为终结点（弧尾），称这条边为弧（arc），此时的图为有向图。若当P<x,y>∈V时必有P< y, x >∈V，则E是对称的，结点x、结点y不分起始和终结，此时以无序对(x,y)来表示x与y之间的一条边，这样的图称为无向图。如图1所示。

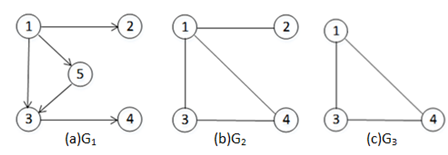
图1 有向图和无向图

图1(a)中的G1为有向图，根据定义可表述为：G1 = (V1,E1)，其中：V1为端点的集合，V1={v1,v2,v3,v4,v5}；E1为弧的集合，E1={< v1, v2>,< v1, v5>,< v1, v3>,< v3, v4>,< v5, v3>}。（图中1、2、3等序号对应的顶点即为v1,v2,v3，之后使用数字表示顶点的图遵循同样的规则）。

图1(b)中的G2为无向图，根据定义可表述为：G2 = (V2,E2)，其中：V2为端点的集合，V2={v1,v2,v3,v4}；E2为边的集合，E2={(v1,v2),(v1,v3),(v1,v4),(v3,v4)}。

（2）完全图

若一个无向图中的每两个顶点之间都存在一条边，则称这个无向图为无向完全图（如图2(a)中的G1）。假设图中顶点的数目为n，显然，无向完全图包含n(n-1)/2条边。

图2 完全图

若一个有向图中的每两个顶点都存在方向相反的两条弧，则称该图为有向完全图（如图2(b)中的G2）。假设图中顶点的数目为n，显然，有向完全图包含n(n-1)条边。

（3）顶点的度

顶点的度（degree）是指依附于某顶点vi的边数，通常记为TD(vi)。

在无向图中，依附于某顶点的边的数目称为该顶点的度。如图7-1(b)中，顶点v1的度为：TD(v1)=3；顶点v2的度为：TD(v2)=1；无向图G2的度为8。

在有向图中，度又分为出度和入度：以顶点vi为弧头的边的数目，称为顶点vi的出度,记为OD(vi)；以顶点vi为弧尾的的边的数目，称为顶点vi的入度，记为ID(vi)。顶点vi的出度与入度之和，称为顶点vi的的度。如图7-1(a)中顶点v3的出度为：OD(v3)=1，入度为： ID(v3)=2；则顶点v3的度为TD(v3)=3。

假设图中顶点的数目为n，边的数目为e，每个顶点的度为di（0 i n-1）,则有：

也就是说，一个图中所有顶点度的和等于图中边的数目的两倍，这是因为图中的每条边连接两个邻接点，在计算度时分为出度和入度计算了两次。

（4）稠密图、稀疏图

若一个图的边数很多，接近完全图，称其为稠密图。反之，若一个图的边数很少（e<nlogn），称其为稀疏图。

（5）子图

假设有两个图分别为G=(V,E)和G′=(V′,E′)，若V′*是V的子集，E′是E的子集，则称图G′是图G的子集。如图1(c)中G3为1(b)中G2的子图。

（6）边的权、网图

与边或者弧有关的数据信息称为权（weight）。在现实生活中，这些权可以表示各种各样的信息。例如，在地铁交通系统中，两个顶点之间边上的权可以表示两站之间的距离，或者两站交通花费的时间；在一个电子线路图中，边上的权值可以表示两个顶点之间的电阻、电流或者电压等。

边上带有权值的图称为网图或者网络（network）。如图3(a)中的G1为有向网图，3(b)中的G2为无向网图。

图3 网图

（7）路径、路径长度、简单路径

存在一个图G=(V,E)，从一个顶点p到另一个顶点q的路径为一个顶点序列，假设这个序列为(p,v1,v2,…,vn,q)。若图G是无向图，则边(p,v1)、(v1,v2)、…、(vi,vj)、…、(vn-1,vn)、(vn,q)属于E(G)。若图G是有向图，则边<p,v1>、<v1,v2>、…、<vi,vj>、…、<vn-1,vn>、<vn,q>属于E(G)。

路径长度指一条路径上经过的边的数目。如图3(a) G1中的路径A(v1,v3,v4)和路径B(v1,v5,v3,v4)，是从顶点v1到v4的两条路径，路径长度分别为2和3。

若一条路径上除去起点和终点，其余顶点各不相同，则称此路径为简单路径。如上文提到的路径A和路径B，都是简单路径。

（8）回路（环）、简单回路

若在一条路径上起点和终点为同一个顶点，则称这条路径为回路或者环。起点与终点相同的简单路径称为简单回路或者简单环。

（9）平行边、重数、自环、简单图

在无向图中，如果关联一对顶点的无向边多于一条，则称这些边为平行边，称平行边的条数为重数。

在有向图中，如果关联一对顶点的有向边多于一条，且方向相同，则称这些边为平行边。

自环是一条边的起点和终点为同一个顶点的边。

既不含平行边也不含自环的图称为简单图。

（10）连通、连通图、连通分量

在无向图中，若顶点p到顶点q之间有路径，则称顶点p和顶点q是连通的。若G中任意两个顶点都连通，则称无向图G为连通图。无向图G中的极大连通子图称为连通分量。显然，连通图中只有一个连通分量，即它本身；非连通图中有不止一个连通分量。图4中给出了非连通图G与它的连通分量示例。

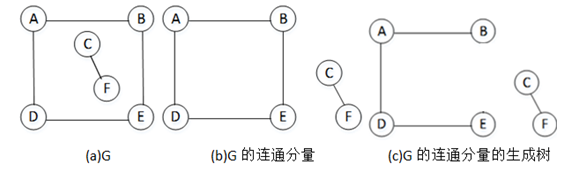
图4 连通分量、生成树、生成森林

（11）强连通图、强连通分量

在有向图中，若任意两个顶点p、q之间，既存在从p到q的路径又存在从q到p路径，则称这个有向图为强连通图。有向图的极大强连通子图称为强连通分量。与连通图相同，强连通图中只有一个连通分量，即它本身；非强连通图中有不止一个连通分量。

（12）生成树

一个连通图的生成树，是包含了该连通图中全部顶点的一个极小连通子图。图的生成树不唯一。从不同的顶点出发进行遍历，可以得到不同的生成树。生成树必定包含连通图中的n-1条边，并且在这棵生成树上任意添加一条边（这条边是连通图G中包含的边），必定构成回路。图4(c)中给出了G的生成树示例。

需要注意的是，具有生成树的图一定是连通的。

（13）生成森林

在非连通图中，每个连通分量都可得到一个极小连通子图，即可以得到一棵生成树，这些连通分量的生成树就组成了一个非连通图的生成森林。如图4(c)就是非连通图G的生成森林。