二叉排序树

在前面几节中，我们学习的都是线性表的查找，除了线性表之外，在非线性的树、图等数据结构中也会经常用到查找算法。经常参与查找的树结构有二叉排序树、平衡二叉树、B树、B+树、键树等，它们统称为树表，本节就来学习一下这些查找树。首先学习针对二叉排序树的查找。

二叉排序树（Binary Sort Tree）又称为二叉查找树、二叉搜索树，它或者是一棵空树，或者是具有下列性质的二叉树：

（1）如果左子树不为空，则左子树上所有结点的值均小于它根结点的值；

（2）如果右子树不为空，则右子树上所有结点的值均大于它根结点的值；

（3）左、右子树也分别为二叉排序树；

（4）树中没有值相同的结点；

如图1，就是一棵二叉排序树。

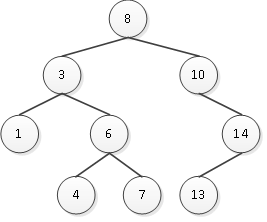
图1 二叉排序树

如果用中序遍历来遍历二叉排序树，则遍历结果是一个递增的序列，例如中序遍历图1中的二叉排序树结果为1 3 4 6 7 8 10 13 14，是一个递增序列，这也是二叉排序树的一个性质特点。二叉排序树通常用二叉链表存储，其结点结构定义如下所示：

typedef struct BitNode
{
  DataType data; //数据域
  struct BitNode* lchild, *rchild, *parent; //左右孩子指针与父结点指针
}BitNode;

一般二叉排序树都是用二叉链表示法存储，但是二叉树的插入删除操作中会用到其父结点指针，因此在其存储结构中增加一个父结点指针parent。

在了解了什么是二叉排序树后，下面来学习一下二叉排序树上的一些常用操作，二叉排序树的查找、插入、删除。

1、查找

二叉排序树最主要的功能就是查找，在二叉排序树中进行查找的基本思路如下所示：

（1）将给定值key与根结点值相比较，如果相等，则查找成功！

（2）如果不相等，则比较key与根结点值的大小：

key大于根结点的值，则在右子树中查找；

key小于根结点的值，则在左子树中查找；

（3）在左/右子树中查找key时，重复上述两个步骤。

二叉排序树的查找是递归的，递归思想在二叉树中的应用非常重要。在实现二叉排序树的查找算法时也用递归来实现，其代码如下所示：

//查找,参数：f指向T的双亲，若查找成功，则p指向该数据元素结点，返回1；
//否则，指针p指向查找路径上访问的最后一个结点，返回-1；
BiTree searchBST(BiTree T, int key, BiTree f, BiTree* p)
{
 if (!T) //树为空
  {
​    *p = f;
​    return NULL;
  }
  else if (T->data == key) //查找成功
  {
​    *p = T;
​    return T;
  }
  else if (T->data > key) //在左子树中查找
​    return searchBST(T->lchild, key, T, p);
  else          //在右子树中查找
​    return searchBST(T->rchild, key, T, p);
}

在二叉排序树中进行查找和折半查找有些类似，也是一个逐步缩小查找范围的过程。若查找成功，则是一条由根结点到待查结点的路径；若查找失败，则是一条由根结点到某个叶子结点的路径；由此可知，查找过程中和关键字比较的次数不超过树的深度。

二叉排序树的平均查找长度与树的形态有关。最好的情况是二叉排序树形态比较对称，此时它与折半查找相似，此时算法的时间复杂度大约为O(log2n)；最坏的情况是二叉排序树是一棵单支树（只有左子树或只有右子树），那么它的查找算法复杂度为O(n)。

2、插入

二叉排序树在生成时，常常需要逐个插入结点，在二叉排序树中插入新的结点，要保证插入后的二叉树仍符合二叉排序树的定义。

（1）如果二叉排序树为空，则为待插入的结点key申请一个新结点，并使其为根；

（2）如果二叉排序树T不为空，则将key与根结点值作比较：

如果两者相等，则说明树中已有此关键字，无须再插入；

如果key<T->key，则将key插入到根的左子树中；

如果key>T->key，则将它插入根的右子树中；

（3）子树中的插入与上述过程一样，如此递归下去，直到将key作为一个新的叶子结点插入到二叉排序树中或者直到发现树中已有此关键字为止。

插入算法在实现的时候可以调用已经实现的查找算法，先在二叉排序树中查找是否存在值为key的结点，如果存在，则直接返回不必再插入；如果不存在，则比较key与根结点的值，判断是插入左子树中还是右子树中，其代码如下所示：

//在二叉排序树T中插入值key
int InsertBST(BitNode *T, int key)
{
  BitNode* p, *s;
  if (!searchBST(T, key, NULL, &p)) //查找不成功，即树中没有值为key的结点
  {
​    s = (BitNode*)malloc(sizeof(BitNode)); //为key分配空间
​    s->data = key;
​    s->lchild = s->rchild = NULL;
​    if (!p) 
​      T = s; //插入s为新根结点
​    else if (key < p->data)
​      p->lchild = s; //s为左孩子
​    else
​      p->rchild = s; //s为右孩子
​    return 1;
  }
  else
​    return 0;
}

​ 有了插入算法，就可以生成一棵二叉排序树，每插入一个结点数据，就调用一次插入算法将它插入到当前已生成的二叉排序树中。

​ 二叉排序树在生成时，其实质是对数据序列进行排序，使其变为有序序列。但这种排序的时间复杂度为O(nlgn)。对于相同的输入实例，它的排序时间是堆排序时间的2至3倍，因此在一般情况下，构造二叉排序树的目的并非为了排序，而是用它来加速查找，因为在有序集合上的查找要比无序集合上的查找更快。

3、删除

在二叉排序树中删除一个结点，也要保证删除结点后的二叉排序树具有原来所有的性质，如果只是删除叶子结点，那么对二叉排序来说不会有什么影响，但若是要删除有孩子的结点，那么情况就比较复杂，基于此，在二叉排序树中删除结点要分三种情况进行讨论：

第一种情况：若结点为叶子结点，即左右子树均为空，由于删除叶子结点不破坏整棵树的结构，则只修改其父结点的指针即可。例如图8-14中的二叉排序树，要删除结点4，则只需将结点6的lchild指向空即可，二叉排序树还是保持原来的性质不变。

第二种情况：若结点只有左子树或只有右子树，则只需要让其左/右子树代替父结点的位置，这也不会破坏二叉排序树的特性。例如要删除图8-14中的结点14，则将14的左孩子13放在结点14的位置上即可。

​ 第三种情况：若结点左右子树都不为空，则在删除时会比较麻烦，假如要删除的结点为p，一种方法是找到其中序遍历的前驱结点pre，用pre替代结点p（即将pre结点的值复制到p结点），然后将pre删除。例如要删除图8.14中的结点6，则先找到其中序前驱结点4，然后用4将6替换，再将4删除，如图2所示。这样二叉排序树还是保持原来的性质不变。

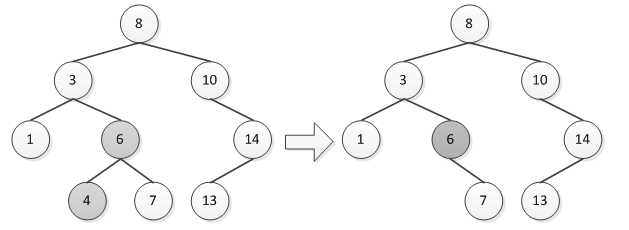
图2 删除结点6

另一种方法是找到结点p的中序后继结点next，则用next替换掉p，再将next删除，也能保持原来的二叉排序树性质不变。同样是删除图1中的结点6，则其中序后继结点为7，用结点7替换结点4，然后将结点7删除，如图3所示。

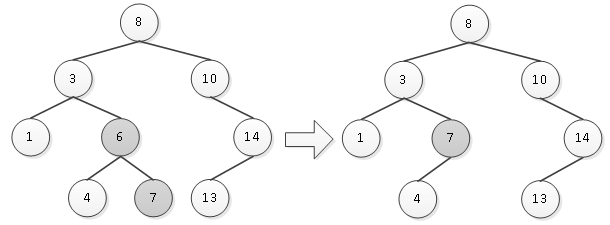
图3 删除结点6

在删除二叉排序树的某一个结点时，这三种情况都要考虑，实现时，利用上面已经有的查找算法，先在二叉排序树中查找是否存在要删除的结点，如果有则需要分三种情况考虑，算法代码如下所示：

void DeleteBST(BitNode* T, int key)
{
    //先在树中查找是否存在值为key的结点
    BitNode* q, *s;
    BitNode* node = searchBST(T, key, NULL, &s); //查找这个结点
    if (node == NULL)
    {
        printf("\n树中没有此结点！\n");
        return;
    }
    else //如果树中存在值为key的结点
    {
        if (node->lchild == NULL && node->rchild == NULL) //如果是叶子结点，则删除
        {
            printf("此结点是一个叶子结点，删除！\n");
            node->parent->lchild = node->parent->rchild = NULL;
            free(node);
        }
        else if (node->rchild == NULL)  //如果右子树为空，只需要重新连接它的左子树
        {
            printf("此结点只有左子树，删除!\n");
            q = node;                      //q指针指向node结点，即要删除的结点
            node = node->lchild; //node移到至其左孩子结点处
            //父结点与孙子结点连接
            if (q == q->parent->rchild) //如果q是其父结点的右孩子
                q->parent->rchild = node; 
            else
                q->parent->lchild = node;

            free(q);
        }
        else if (node->lchild == NULL) //如果左子树为空，只需要重新连接它的右子树
        {
            printf("此结点只有右子树，删除!\n");
            q = node; 
            node = node->rchild;
            if (q == q->parent->rchild) //如果q是其父结点的右孩子
                q->parent->rchild = node; //则将其右孩子挂在父结点的右侧
            else
                q->parent->lchild = node;
            free(q);
        }
        else  //如果结点左右子树均不为空
        {
            q = node;
            s = node->lchild;             //s指向其左子树
            //寻找其中序前驱，其中序前驱在其左子树的右下角
            while (s->rchild)             //在左子树中往右边找
            {
                q = s;
                s = s->rchild;
            }
            //循环结束，s就指向要删除结点的中序前驱
            node->data = s->data;         //将s结点的数据复制到node结点
            if (q != node)
                q->rchild = s->lchild;
            else
                q->lchild = s->lchild;
            free(s);
        }    
    }
}

二叉排序树是以链式方式进行存储，它保持了链式存储在执行插入删除时只修改指针，不移动元素的优点。至此，二叉排序树查找、插入、删除操作原理、相应算法的实现及算法复杂度的分析已经学习完毕。当然，每种算法也可有不同的实现，读者可在课下尝试自己来实现二叉排序树的相关算法。